Zurück Index
Weiter
3. Ein einfaches Beispiel
Ein Beispiel, welches möglicherweise schon zu typisch
für OO ist, sich aber sehr gut eignet ein paar einfache Sachverhalte
darzustellen, ist eine einfache Verwaltung primitiver geometrischer Objekte.
3.1 Die Klassen werden gesucht
In diesem Fall wird ein großer Teil eines möglichen
Endproduktes (zum Beispiel ein Zeichenprogramm) ausgelassen, und eben nur
die Verwaltung einiger primitiver Datenobjekte modelliert. Das kann beispielhaft
für die grundlegende Vorgehensweise aller Methoden stehen, und dem
Bereich OOA zugerechnet werden. Die zu modellierenden geometrischen Objekte
sind Rechteck, Quadrat, Kreis, Ellipse, Gerade und ein einfacher Kurvenzug
der von Kontrollpunkten gestützt wird.
Alle diese Elemente sind geometrische Objekte, die in
Bezug auf Größe, Position, Farbe usw. bestimmt sind, doch das
einzige, was ihnen gemeinsam ist, ist die Position, zu der alle weiteren
geometrischen Eigenschaften relativ sind, und eine Farbe. Diese Gemeinsamkeit
reicht freilich nicht, um daraus ein konkretes geometrisches Objekt ableiten
zu können (was sollte es sein?). Also scheint eine abstrakte
Basisklasse "GeomObjekt" (von der keine Instanzen erzeugt werden
können) nahezuliegen, die sich weiterhin durch Attribute
(Datenelemente) und Operationen (Methoden) auszeichnet. Bei
"GeomObjekt" lägen "position" und "farbe" als Attribute und "verschieben()",
"skalieren()", "zeigen()", "verstecken()" und "setzeFarbe()" als Operationen
nahe, die bei allen geometrischen Objekten einen Sinn ergeben (siehe Abb.
6).
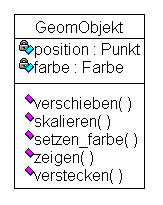 Abb. 6
Abb. 6
Operationen zum Erzeugen (Konstruktor),
Vernichten (Destruktor), Zuweisen oder Vergleichen können
nach Vereinbarung vorausgesetzt werden und werden üblicherweise in
Diagrammen nicht vermerkt. Außerdem sei auf die von C bekannte Schreibweise
eines Funktions- oder Methodennamens hingewiesen, die nicht nur hier hilft,
Attribute von Operationen zu unterscheiden, sondern auch in einigen Notationen
übernommen wurde. Es ist überdies üblich Klassen- oder auch
Objektnamen groß, Attribut- und Operationennamen aber klein zu schreiben.
Obwohl alle oben genannten Attribute und Operationen allen
plausiblen geometrischen Objekten gemeinsam sind, macht es keinen Sinn,
die Operation "skalieren()" zu spezifizieren, da die Art, in der die geometrischen
Informationen der einzelnen Objekttypen abgelegt werden, noch unbekannt
ist. Diese Operation ist abstrakt (virtuell) und wird erst
bei abgeleiteten Klassen konkretisiert.
Auch wenn es in einem so primitiven Beispiel keinen Sinn
macht, von OOA und OOD zu reden, sei es jedoch
angemerkt, daß bisher fast alle modellierten Objekte letztlich zum
Problembereich eines Projektes "Zeichenprogramm" gehören. Wie ist
es jedoch mit den Operationen zeigen() und verstecken()? Sollte eine selektive
Darstellung der Objekte nicht zur Spezifikation der Aufgabe "Zeichenprogramm"
gehören, so sind diese Funktionen lediglich Hilfsmittel für andere
Operationen wie zum Beispiel verschieben(), damit also Teil des Lösungsbereiches
und so eher Aufgabe des OOD.
Überdies sollten im Sinn des Geheimhaltungsprinzips
noch weitere Operationen in die jeweiligen Klassen eingebettet werden,
die einen Zugriff oder vielmehr eine Abfrage der eigentlich geschützten
Attribute ermöglichen. Dies gehört sicherlich auch in den Lösungsbereich,
soll hier aber ausgelassen werden.
3.2 Etwas mehr Detail
Eine erste Spezialisierung wäre nun eine von GeomObjekt
abgeleitete Klasse der graphischen Objekte mit einem von Null verschiedenem
Flächeninhalt ("ObjectFläche") und eine Klasse der Objekte die
"linienähnlich" sind ("ObjectLinie"), da den flächigen Objekten
nun noch ein Attribut füllfarbe und den linienähnlichen Objekten
ein Attribut endpunkt zugefügt werden kann (siehe Abb.
7).
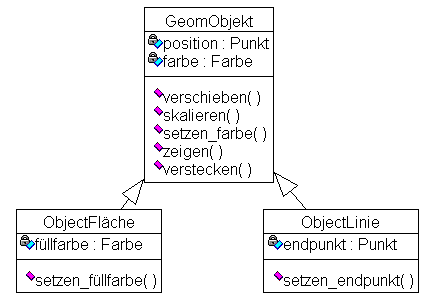 Abb. 7
Abb. 7
Beide abgeleiteten Klassen sind ihrerseits jedoch wieder
abstrakt. Deswegen wird jetzt eine erste nicht-abstrakte Klasse "Gerade"
und eine Klasse "Kurve" eingeführt. Kurve zeichnet sich durch den
Typ aus, der der mathematischen Berechnung zu Grunde liegt, und enthält
noch vier Kontrollpunkte.
Desweiteren werden von den beiden Flächenobjekten
eine Klasse der kreisförmigen und eine der rechteckigen Objekte und
ihre jeweilige Spezialisierung abgeleitet (siehe Abb.
8).
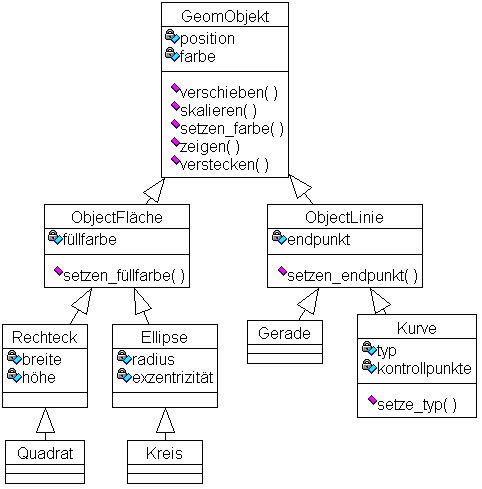 Abb. 8
Abb. 8
3.3 Die Unified Modeling Language
Nun, da eigentlich die geplanten Größen in einem
Klassendiagramm modelliert wurden, ein paar Worte zur verwendeten Notation.
Die bisher dargestellten Größen waren natürlich
alles Klassen, die hier durch eine einfache Box mit drei Abteilungen, eine
für den Namen, eine für Attribute und eine für Operationen,
dargestellt wurden. Diese Art der Notation entspricht den Konventionen
der Unified Modeling Language. Die Vererbungshierarchie wird von der UML
als Generalization-(Verallgemeinerungs-) Relation bezeichnet, der Pfeil
geht dementsprechend von der spezialisierten zur verallgemeinerten Klasse.
Die Bezeichnung Attribute für Datenelemente einer Klasse und Operationen
für Methoden entspricht auch der UML.
Fast alle OO-Methoden bringt auch eigene Notationen mit
sich, die sich rein äußerlich mehr oder weniger voneinander
unterscheiden (siehe Abb. 9 ; mehr zu den einzelnen
Symbolen später). Da die zu modellierenden Sachverhalte aber sehr
ähnlich sind, läßt sich die eine Darstellung oft direkt
in die andere überführen.
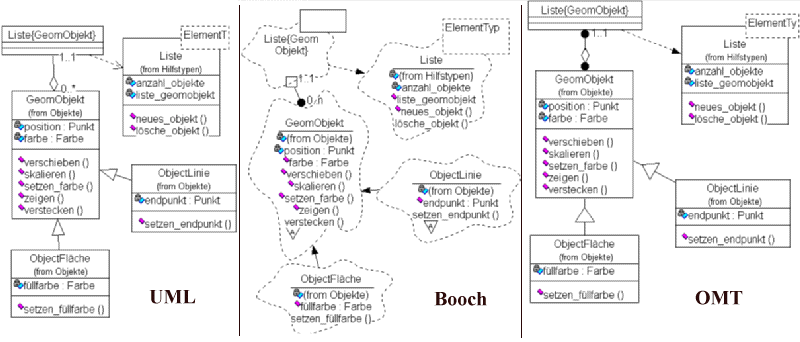 Abb. 9 Notationsvergleich
Abb. 9 Notationsvergleich
Obwohl die Notation von Coad-Yourdon
in Lehrbüchern offensichtlich sehr beliebt ist, suchte man im industriellen
Bereich wohl nach einer weiteren Lösung für das Problem der Notationsvielfalt.
Die Vertreter von OOD (Booch), OMT
(Rumbaugh) und OOSE (Jacobson), die mittlerweile
gemeinsam die Firma Rational gegründet hatten, bemühten sich
um eine Standardisierung und entwarfen die Unified Method, aus deren Notation
schließlich die Unified Modeling Language wurde. Die
in Dokumenten zur Unified Method vorgeschlagene Notation unterscheidet
sich im Detail etwas von UML. Die Unified Modeling Language enthält
Elemente sowohl aus OOD, OMT, OOSE als
auch aus anderen Notationen.
Zurück
Index Weiter




