The thinnest densest two-dimensional packing ??
On this page I consider the problem of finding the centraly symmetric convex
area whose densest packing is the thinnest. Reinhardt and Mahler describe in
their works a possible candidate for this problem: The smoothed octagon.
It is obtained by taking a regular octagon and smoothing the edges with
a hyperbola which touches the adjecent edges of the octagon and which has
the edges adjacent to these edges as asymptotes. (see L.F. Toth, Lagerungen in der Ebene auf der Kugel und im Raum p. 104)
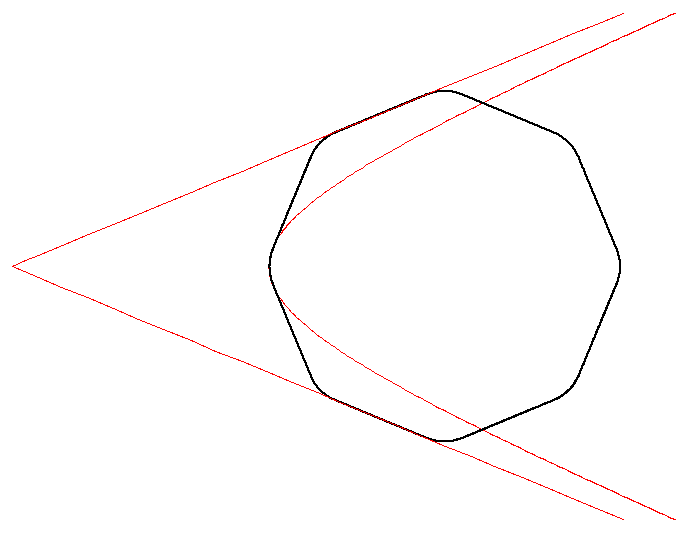 The equation which describes the hyperbola is l²x²-m²=y², with
l=sqrt(2)-1, m=sqrt(6*sqrt(2)-8)*(sqrt(2)+1)/2. The edges of the octagon
touched by the hyperbola lie on y=±(sqrt(2)+1)*(x-2), with x›=2.
The asymptotes of the hyperbola are y=±l*x.
The equation which describes the hyperbola is l²x²-m²=y², with
l=sqrt(2)-1, m=sqrt(6*sqrt(2)-8)*(sqrt(2)+1)/2. The edges of the octagon
touched by the hyperbola lie on y=±(sqrt(2)+1)*(x-2), with x›=2.
The asymptotes of the hyperbola are y=±l*x.
The densest packing of this area is the following:
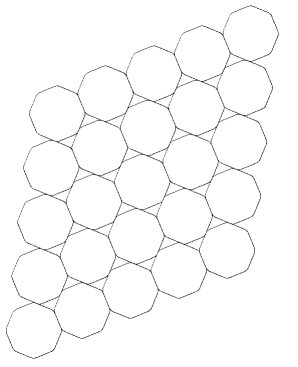 To every octagon, there are two holes. If the packing contains regular
octagons of edgelength e, the area of a hole, with two edges of length
e/sqrt(2) and one of length e, is e²/4. The area of the octagon with
edgelength e is
2e²/(sqrt(2)-1). The density is now simple to compute. One gets for
the density: 4/(3+sqrt(2)) = 0.90616... . If you consider the
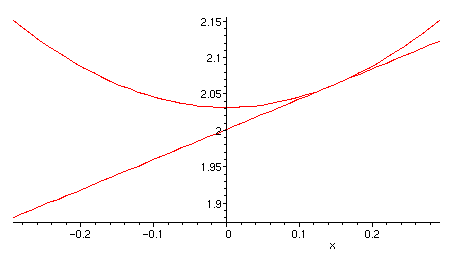
smoothed octagon, you get for the density (for example by integrating
the formula for the hyperbola. See following picture):
(9 - sqrt(32) - ln(2))/(sqrt(8)-1) =
0.90241... . Probably this is the thinnest tightest two-dimensional
Packing and the density of the densest packing of any convex area is
greater or equal than this value.
To every octagon, there are two holes. If the packing contains regular
octagons of edgelength e, the area of a hole, with two edges of length
e/sqrt(2) and one of length e, is e²/4. The area of the octagon with
edgelength e is
2e²/(sqrt(2)-1). The density is now simple to compute. One gets for
the density: 4/(3+sqrt(2)) = 0.90616... . If you consider the
smoothed octagon, you get for the density (for example by integrating
the formula for the hyperbola. See following picture):
(9 - sqrt(32) - ln(2))/(sqrt(8)-1) =
0.90241... . Probably this is the thinnest tightest two-dimensional
Packing and the density of the densest packing of any convex area is
greater or equal than this value.
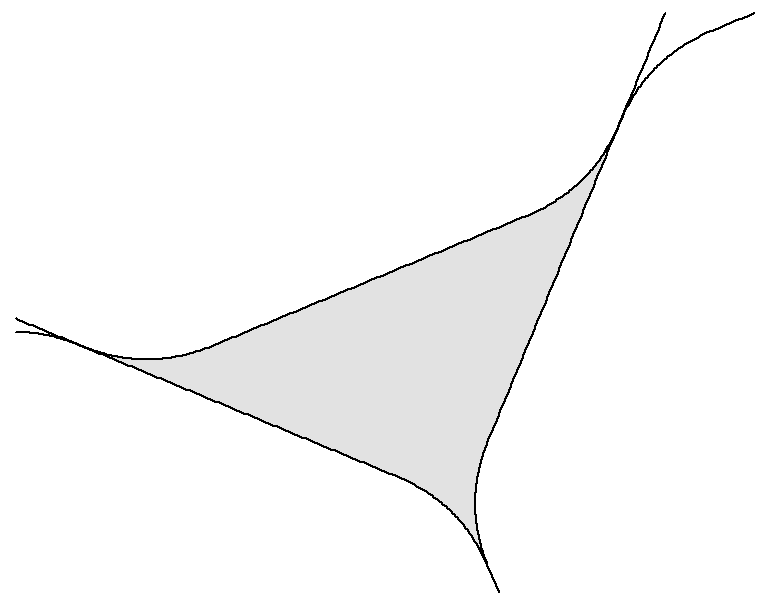
A closer look at a hole of this packing:
 Peter Scholl
(Peter.Scholl@unix-ag.org)
(last modified: 02.05.2001)
Peter Scholl
(Peter.Scholl@unix-ag.org)
(last modified: 02.05.2001)





 Peter Scholl
(Peter.Scholl@unix-ag.org)
(last modified: 02.05.2001)
Peter Scholl
(Peter.Scholl@unix-ag.org)
(last modified: 02.05.2001)